Motion is all around us. Understanding displacement, velocity, acceleration, and kinematic equations is crucial in physics. This guide will provide detailed explanations, real-world examples, graphical interpretations, and AP Physics-style practice problems to build confidence in solving kinematics questions.
What is Kinematics?
Kinematics is the study of motion without considering forces that cause it. It focuses on describing how an object moves using:
- Displacement () – How far an object moves from its starting position.
- Velocity () – How fast and in which direction an object moves.
- Acceleration () – The rate at which velocity changes.
These concepts are best understood visually through graphs.
Understanding Displacement
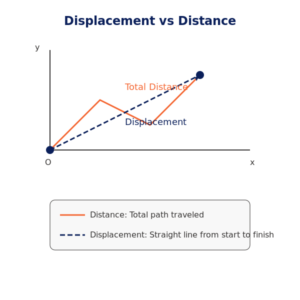
Difference Between Displacement and Distance
| Concept | Definition | Example |
|---|---|---|
| Distance | The total path traveled, regardless of direction. | A person walks 10m east, then 5m west. Distance = 15m. |
| Displacement () | The shortest straight-line change in position, including direction. | A person walks 10m east, then 5m west. Displacement = 5m east. |
Key Point: Distance is a scalar (magnitude only), while displacement is a vector (magnitude + direction).
Displacement Formula & Example
Where:
- = Final position
- = Initial position
Example:
A car moves from position to .
So, displacement = 8m forward.
Velocity: How Fast and in Which Direction?
Velocity describes both speed and direction.
Average Velocity vs. Instantaneous Velocity
| Type | Definition | Example |
|---|---|---|
| Average Velocity | Total displacement divided by total time. | A plane travels 500 km north in 2 hours. The average velocity is 250 km/h north. |
| Instantaneous Velocity | The velocity at a specific instant. | A car’s speedometer shows 60 mph at a particular moment. |
Velocity Formula & Example
Where:
- = Velocity
- = Displacement
- = Time interval
Example:
A cyclist moves 50m east in 5s.
Velocity is 10 m/s east.
Acceleration: Changing Velocity Over Time
Acceleration measures how velocity changes over time.
Acceleration Formula & Example
Where:
- = Acceleration
- = Change in velocity
- = Time taken
Example:
A car speeds up from 0 m/s to 20 m/s in 4s.
Acceleration is forward.
The Four Kinematic Equations

For additional physics concepts, check College Board AP Physics 1 Course Guide.
AP Physics-Style Questions & Solutions
Below are 10 high-quality AP Physics-style kinematics questions, covering different difficulty levels. Each question has a detailed solution so you can learn step by step.
Question 1: Finding Velocity
A car starts from rest and accelerates at 3 m/s² for 6 seconds. What is its final velocity?
Solution:
Using the first kinematic equation:
So, the car’s final velocity is 18 m/s.
Question 2: Calculating Displacement with Acceleration
A runner accelerates at 2 m/s² from rest for 5 seconds. How far does he travel?
Solution:
Using the second kinematic equation:
The runner travels 25 meters.
Question 3: Motion in Free Fall
A ball is dropped from a height of 80 meters. How long does it take to reach the ground?
Solution:
Using the second kinematic equation:
Since the ball is dropped, , and .
The ball reaches the ground in 4.04 seconds.
Question 4: Finding Final Velocity Without Time
A motorcycle accelerates at 4 m/s² over a distance of 50m, starting from rest. What is its final velocity?
Solution:
Using the third kinematic equation:
The final velocity is 20 m/s.
Question 5: Average Velocity Calculation
A car moves 100 meters east in 10 seconds, then 50 meters west in 5 seconds. What is its average velocity?
Solution:
Total displacement:
Total time:
Average velocity is 3.33 m/s east.
Question 6: Catching Up Problem
A train moving at 10 m/s passes a station. 5 seconds later, another train starts from rest and accelerates at 2 m/s². How long does it take for the second train to catch up?
Solution:
The distance the first train has traveled before the second train starts:
Using the second kinematic equation for the second train:
Since :
Total time from when the first train passed the station:
The second train catches up in 12.07 seconds.
Question 7: Graph-Based Question
A velocity vs. time graph shows a straight line starting from 0 m/s and reaching 30 m/s in 6 seconds. What is the acceleration?
Solution:
Slope of a velocity vs. time graph gives acceleration:
Acceleration is 5 m/s².
Question 8: Braking Distance
A car traveling at 20 m/s suddenly brakes with an acceleration of -4 m/s². How far does it take to stop?
Solution:
Using the third kinematic equation:
The car stops after 50 meters.
Question 9: Elevator Motion
An elevator starts from rest and moves upward with an acceleration of 1.5 m/s² for 4 seconds. What is its velocity at the end?
Solution:
Using :
Final velocity is 6 m/s upward.
Question 10: Maximum Height of a Thrown Object
A ball is thrown straight up at 15 m/s. How high does it go?
Solution:
Using the third equation with at max height:
The ball reaches 11.48 meters.
These 10 questions cover every kinematics concept, making you more confident in solving AP Physics 1 problems.
Understanding kinematic equations is essential for solving motion-related problems in physics. By breaking down displacement, velocity, and acceleration, we’ve seen how these concepts work together to describe how objects move.
The four kinematic equations provide powerful tools for solving a wide range of motion problems, whether it’s a car accelerating on a highway, a ball in free fall, or a train catching up to another.
Key Takeaways:
✔ Displacement measures how far an object moves, considering direction.
✔ Velocity includes both speed and direction, making it different from speed.
✔ Acceleration describes how quickly velocity changes over time.
✔ Graphs (Position-Time, Velocity-Time, Acceleration-Time) provide insights into motion.
✔ Kinematic equations allow us to predict an object’s future position and velocity under constant acceleration.
To excel in AP Physics, practice solving problems using these equations. Try different types of motion scenarios—objects speeding up, slowing down, or moving at a constant velocity. The more you practice, the more intuitive these concepts will become.
For more AP Physics 1 study guides, practice problems, and tutoring, visit:
- Refresh Kid – AP Physics 1 tutoring and courses.
- Refresh Kid Blog – Exam tips, study strategies, and resources.
If you’re preparing for the AP exam, revisiting these concepts and practicing AP-style questions will build confidence and help you solve motion problems efficiently.
Physics is not about memorizing formulas—it’s about understanding motion! Keep practicing, analyzing, and questioning, and soon, solving kinematics problems will feel like second nature.



